Best First Search (BFS)
BFS is an algorithm that combines the depth-first and breadth-first search strategies. Using both algorithms' benefits is made possible by it. Its methods include search and the heuristic function. At each phase, we can select the most promising node with the aid of the best-first search.
One path is followed at a time in the Best First Search approach, but paths are swapped when a more promising path than the one being followed is discovered.
Algorithm Best First Search
- Step 1: Add the initial node to the list of OPEN list
- Step 2: Stop and return failure if the OPEN list is empty
- Step 3: Transfer the node n (which has the lowest value of h(n)) from the OPEN list to the CLOSED list
- Step 4: Compute the successors of node n and expand node n
- Step 5: Examine every node that comes after node n to determine if it is a goal node or not. Proceed to the next stage if none of the successor nodes are the goal node; otherwise, return success and end the search
- Step 6: The algorithm looks for the evaluation function f(n) for each successor node, after which it determines if the node has ever been in the OPEN or CLOSED list
- Step 7: Return to step 2
Best First Search Technique Example
We will use greedy best-first search to traverse the search problem below. Every iteration uses the evaluation function f(n)=h(n), which is listed in the table below, to grow each node.
We are using two lists in this search example: the OPEN and CLOSED Lists. The steps for going through the example mentioned above are as follows.
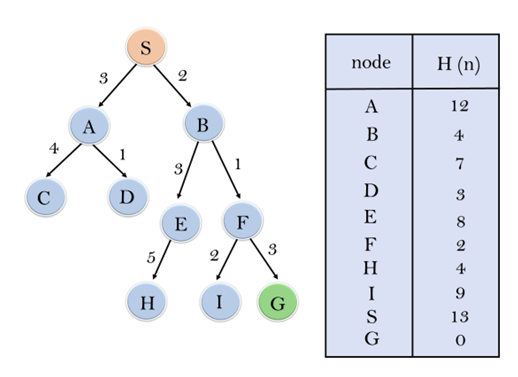
Add S's expanded nodes to the CLOSED list.
Initialization: Open [A, B], Close [S]
Iteration 1: Open [A, E, F], Close [S, B]
Iteration 2: Open [A, E, H, I, G], Close [S, B, F]
Iteration 3: Open [A, E, H, I], Close [S, B, F, G]
Hence the final solution path will be:
S--B--F--G
Time Complexity:
The Greedy best-first search has a worst-case time complexity of O(bm).
Space Complexity:
The Greedy best-first search's worst-case space complexity is O(bm). where m is the search space's maximum depth.
Advantages Of Best First Search (BFS)
- The best first search can switch between BFS and DFS by gaining the advantages of both algorithms.
- This algorithm is more efficient than BFS and DFS algorithms.
- This algorithm is simple and easy to understand.
- This algorithm is fast and efficient.
- BFS algorithm has less memory requirement.
Disadvantages Of Best First Search (BFS)
- It can behave as an unguided depth-first search in the worst-case scenario. It can get stuck in a loop as DFS.
- This algorithm is not optimal.
- In this algorithm requires a heuristic function.
- Some time it provide inaccurate results.


